
Let us consider one hollow circular section, where we can see that D is the diameter of main section and d is the diameter of cut-out section as displayed in following figure. Sol: The given plate is symmetrical about the y-y axis, therefore \ = 150 mm. Today we will see here the method to determine the moment of inertia of a hollow circular section with the help of this post. A differential element of area in the form of a circular ring may be used for the calculation of the moment of inertia about the polar z-axis through O. To find \, we have to divide the whole Figure into standard areas.Įxample: Find the moment of inertia of a plate with a circular hole about its centroidal x axis as shown in Fig.8. The moment of inertia of the shaded area is obtained by subtracting the moment of inertia of the half-circle from the moment of inertia of the rectangle. This is important, since the moment of inertia will vary depending on the axis chosen.
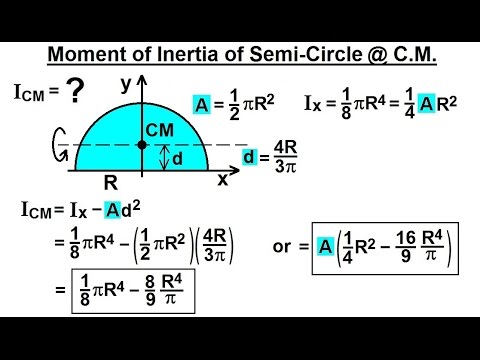
To determine the area moment of inertia, start by drawing out the area under analysis, and include the axes you are taking the moment of inertia about. Sol: The given I-section is symmetrical about the y-y axis, therefore, Calculating the Rectangular Area Moment of Inertia via Integration. = + Įxample: Determine the moment of inertia about the horizontal axis passing through the centroid of the section as shown in Fig.7.


 0 kommentar(er)
0 kommentar(er)
